The “fuzzy” class of the 99%

“We are the 99% and we have credit”… but who we are?

One of the slogans, if not “the” slogan, of the Occupy movement is “We’re the 99%”: some people think we are already dealing with the polarization foreseen by Marx in his “Manifesto”[1]. Politically speaking, the most interesting datum is not the miscellany within the 99% as much as the charge of the 1%.

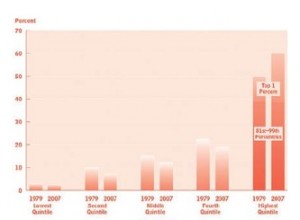
(Picture 1. Doug Henwood, in his article “Is About the %1”, provides a graph of the tangled stratification of the 99% and the nature of the 1% on the whole).

If it is truethat, on a propaganda level, “we are the 99%” is a very effective slogan, actually things are a little bit more complex. On one hand there is a theory (“untimely” [2]) that had singled out a probable historical trend that, in the long term, would have led to the polarization in two classes; on the other, there is the context of a “crisis” that stops to guarantee even the crumbs and that has generated a situation where a 1% has still access to the “crumbs”, while there is a 99% including both who have never had access to the crumbs, and who, because of the crisis, have no more access to them, or who, always because of the crisis, could have no more access in the near future. Finally, the analysis of this situation refers to the statute of the term “class”.

Actually, Marx has never had a chance to work out clearly a theory on social classes: the word “klasse” is often used in the Manifesto, mainly in a propaganda way, but in the Capital the matter of classes (cf. Chapter 52, The Classes ) takes up the last one and a half page, and the treatment has never been completed.

Moreover, in those years the term “klasse” was at the center of a scientific debate on the nature of the “sets”, “mathematical synonym” for “classes”. Georg Cantor (inspired by Spinoza’s pantheism, that provided two “orders” of infinity) was the first to work out a scientific theory of the sets, or classes (the so-called “naive set theory”). His theory, still used today – “carefully” [3] – in mathematical analysis, carried contradictions and antinomies. The philosophic and scientific path of the XX century, developed around the matter of the “foundations of mathematics”, has led, with the fuzzy logic by Lofti Zadeh [4], to a new formulation of the idea of “set”.

However, in Marx’s time the idea of set (scientific version of the concept of “klasse”) was still to be worked out; moreover, as previously said, Marx did not have time to work out a scientific treatment of it. Today we can make use of much more refined scientific tools and we can try to use them in order to clarify the current situation.

In the “classic” set theory, based on a 2-values logic (true/false), a single element can belong or not to belong to a given set; a fuzzy set, instead, is characterized by a function of belonging degree, that associates one element with the set according to a degree of belonging defined in the continuous real interval [0, 1]. This new conceiving of sets can account for both the belonging “in the strict sense” of a person to a social class (set), and for the (not)belonging, in different ways, of a person to a given social class. The dichotomy between working class and owners of the means of production can be singled out between the two “extreme” values 0 and 1: in the middle there is the infinite current stratification (that you find in the well-known 99%).

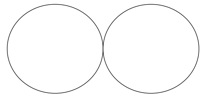
(Picture 2. Graphic representation of two classic sets)

(Picture 3. Graphic representation of two “fuzzy” sets)

The pattern of fuzzy social classes can also account for the historical change and for any passage (if we consider valid the tendential polarization mentioned above in the Manifesto) from one class to another.

These reflections, translated in political terms, are useful to clarify the statute of 99%. The point is the following: the crisis has stopped to guarantee even the crumbs and, so doing, it has produced, as dialectic complement, a political fight ad hoc.

The episode of the arrests on the occupy bridge provides a clear datum on the formation and stratification within the 99%: if occupants on the bridge could be counted in thousands, the arrested were 200, the other, however having something (the last crumbs) to lose, went back thus avoiding the charges.

Therefore, the uncritical enthusiasm for the 99% is unjustified. Nevertheless, the American Occupy! movement has its positive and politically very interesting sides:

1. compared to the political history in USA, it is a novelty and a positive sign of political mobilization

2. though the American law bans communism, the Occupy movement has included anti-capitalism in its platform, and among its reference points there are also declared Marxists as David Harvey

3. though the American law has always banned the organization of an American Communist Party, the Occupy! movement has found its own way to self-organization

4. in some cases, the movement felt the need to have a physical place, and for the first time in USA, it has tried to organize an occupation, calling that place “social centers”

5. apart from the possible developments of the Occupy! movement, it will become famous in the historical memory of American (and international) movement, as an interesting “precedent”.

NOTES:

[1]  “Die gaze Gesellschaft spaltet sich mehr und mehr in zwei große feindliche Lager, in zwei große, einander direkt gegenüberstehende Klassen: Bourgeoisie und Proletariat” (K. Marx-F. Engels, Manifest der Kommunistischen Partei).

[2] Cf. D. Bensaïd, Marx l’intempestif. Grandeurs et miseres d’une aventure critique (XIXe-XXe siecles), Fayard, Paris, 1995.

[3] Mathematical analysis can use the “naive set theory” because it is not touched (for example in the definition of the dominion of a function) by the antinomy of Russel, who disproved Cantor’s theory and, actually, launched one of the epistemological debates that characterize the XX century.

[4] L. Zadeh, Fuzzy sets. Information and Control. 1965; 8: page 338–353.

Bibliography:

A.A.V.V., Occupy! Scenes from occupied America, Verso, 2011
D. Bensaïd, Marx l’intempestif. Grandeurs et miseres d’une aventure critique (XIXe-XXe siecles), Fayard, 1995
G. Cantor, La formazione della teoria degli insiemi: saggi 1872-1883, edited by Gianni Rigamonti, Sansoni, 1992
B. Kosko, Fuzzy Thinking: The New Science of Fuzzy Logic, Hyperion, 1993
L. Zadeh, Fuzzy sets. Information and Control. 1965; 8: page 338–353

Traduzione dell’approfondimento: La classe “fuzzy” del 99%