La classe “fuzzy” del 99%

“Siamo il 99% e siamo in credito”…ma chi siamo?

Uno degli slogan, se non “lo” slogan, del movimento Occupy è “We’re the 99%”: alcuni hanno pensato che si tratti già della polarizzazione prevista da Marx nel “Manifesto” [1].  Il dato politicamente più interessante – e rivendicabile – non è tanto la miscellanea interna al 99% quanto la denuncia dell’%1.
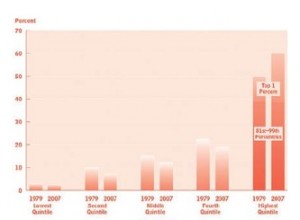(Immagine 1. Doug Henwood, nel suo articolo “Is About the %1”, fornisce un grafico che visualizza, nel suo complesso, l’intricata stratificazione del 99%, e la natura dell’%1).

Se è vero che, tatticamente (a livello di propaganda), “siamo il 99%” è uno slogan che può risultare efficace; le cose, nei fatti, sono un po’ più complesse. Da una parte abbiamo una teoria (“intempestiva”[2])  che aveva individuato una probabile tendenza storica che, sul lungo periodo, avrebbe portato alla polarizzazione in due classi; dall’altra abbiamo il contesto di una “crisi” che sta facendo mancare le briciole, e che ha generato una situazione in cui c’è un 1% che ha ancora accesso alle “briciole”, e un 99% che comprende sia chi non ha mai avuto accesso alle briciole, o, a causa della crisi, non vi ha più accesso, o,  sempre a causa della crisi, in un futuro prossimo potrebbe non avervi più accesso. L’analisi di questa situazione rimanda, in ultima analisi, allo statuto del termine “classe”.
Marx, in realtà, non ebbe mai modo di elaborare a chiare lettere una teoria delle classi sociali: il termine “klasse” è usato spesso nel Manifesto, per lo più in modo propagandistico, ma nel Capitale, la questione delle classi (cfr. Capitolo 52, Le Classi) occupa l’ultima pagina e mezzo, e la trattazione è rimasta incompiuta.
In quegli anni, tra l’altro, il termine “klasse” fu al centro di un dibattito scientifico sulla natura degli “insiemi”, “sinonimo matematico” di “classi”. Georg Cantor (ispirato dal panteismo di Spinoza, che prevedeva due “ordini” di infinito) fu il primo ad elaborare una teoria scientifica degli insiemi, o classi (la cosiddetta “teoria ingenua degli insiemi”). La sua teoria, usata tutt’ora – in modo “prudente” [3] –  nell’analisi matematica, portava con sé contraddizioni e antinomie. Il percorso filosofico e scientifico del ’900, sviluppatosi attorno alla questione dei “fondamenti della matematica”, ha portato, con la logica fuzzy proposta da Lofti Zadeh [4], ad una nuova formulazione del concetto di “insieme”.
Ai tempi di Marx, però, il concetto di insieme (versione scientifica del concetto di “klasse”) era ancora tutto da elaborare; inoltre, come abbiamo detto, Marx non ebbe il tempo di elaborarne una trattazione scientifica. Oggi possiamo avvalerci di strumenti scientifici ben più raffinati e possiamo cercare di utilizzarli per fare chiarezza nella situazione attuale.
Nella teoria “classica” degli insiemi, basata su una logica a 2 valori (vero/falso) un elemento può appartenere o non appartenere a un dato insieme; un insieme fuzzy, invece, è caratterizzato da una funzione di grado di appartenenza, che associa un elemento all’insieme secondo un grado di appartenenza definito nell’intervallo reale continuo [0, 1]. Questa nuova concezione degli insieme riesce a rendere conto sia dell’appartenenza “in senso stretto” di una persona ad una classe (insieme) sociale, sia della (non-) appartenenza, a diverso titolo, di una persona ad una certa classe sociale. La dicotomia tra proletariato e proprietari dei mezzi di produzione può essere individuata nei due valori “estremi” 0 e 1: nel mezzo c’è l’infinita stratificazione attuale (che ritroviamo nel famoso 99%).

(Immagine 2. Rappresentazione grafica di due insiemi classici)

(Immagine 3. Rappresentazione grafica di due insiemi “fuzzy”)

Il modello della classi sociali fuzzy può rendere conto anche del mutare storico e degli eventuali passaggi (se prendiamo per buona la tendenziale polarizzazione di cui sopra nel Manifesto) da una classe all’altra.
Queste riflessioni, tradotte in termini politici, servono a fare chiarezza sullo statuto del 99%. Il punto centrale è il seguente: la crisi ha iniziato a far mancare le briciole e, in quanto tale, ha prodotto, come complemento dialettico, una battaglia politica ad hoc.
L’episodio degli arresti sul ponte occupato dà un chiaro dato sulla formazione e stratificazione interna del 99%: se gli occupanti sul ponte si potevano contare nell’ordine delle migliaia, gli arrestati sono stati 200, gli altri, avendo comunque qualche cosa (le ultime briciole) da perdere, sono tornati indietro evitando le denunce.
L’entusiasmo acritico per il 99% è quindi ingiustificato; ciò nonostante, il movimento americano di Occupy! ha i suoi lati positivi e politicamente molto interessanti:
1) rispetto alla storia politica negli USA, è un’inedito, ed è un segno positivo di mobilitazione politica
2) nonostante la legge americana metta al bando il comunismo, il movimento Occupy ha incluso l’anticapitalismo nella sua piattaforma, e tra i suoi punti di riferimento ci sono anche marxisti dichiarati come David Harvey
3) nonostante la legge americana abbia da sempre vietato l’organizzazione di un Parito Comunista Americano, il movimento Occupy! ha trovato una sua via all’ (auto-) organizzazione
4) in alcuni casi, il movimento ha sentito la necessità di darsi un luogo fisico, e ha cercato, per la prima volta negli USA, di organizzare un’occupazione, chiamando quel luogo “social centres”
5) a prescindere da quelli che saranno gli sviluppi del movimento Occupy, esso restarà, nella memoria storica del movimento americano (e internazionale), un interessante “precedente”.

NOTE:

[1]  “Die ganze Gesellschaft spaltet sich mehr und mehr in zwei große feindliche Lager, in zwei große, einander direkt gegenüberstehende Klassen: Bourgeoisie und Proletariat” (K. Marx-F. Engels, Manifest der Kommunistischen Partei).
[2] Cfr. D. Bensaïd, Marx l’intempestif. Grandeurs et miseres d’une aventure critique (XIXe-XXe siecles), Fayard, Parigi, 1995.
[3] L’analisi matematica può usare la teoria “ingenua” degli insiemi perché non viene toccata (ad esempio nella definizione nel dominio di una funzione) dall’antinomia di Russell, che invalidò la teoria cantoriana, e, di fatto, lanciò uno dei dibattiti epistemologici che ha caratterizzato il ’900.
[4] L. Zadeh, Fuzzy sets. Information and Control. 1965; 8: pagg. 338–353.

Bibliografia:

A.A.V.V., Occupy! Scenes from occupied America, Verso, 2011
D. Bensaïd, Marx l’intempestif. Grandeurs et miseres d’une aventure critique (XIXe-XXe siecles), Fayard, 1995
G. Cantor, La formazione della teoria degli insiemi: saggi 1872-1883, a cura di Gianni Rigamonti, Sansoni, 1992
B. Kosko, Fuzzy Thinking: The New Science of Fuzzy Logic, Hyperion, 1993
L. Zadeh, Fuzzy sets. Information and Control. 1965; 8: pagg. 338–353

Leggi anche: The “fuzzy” class of the 99%